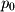
The parametric forms of lines and planes are probably the most intuitive forms to deal with in linear algebra. Parametric definitions rely on linear combinations of a starting point with N direction vectors. The number of direction vectors is equal to the dimension of the geometric object. So a line has 1 direction vector, a plane has 2, and a hyperplane has 3 or more:
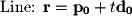
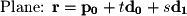
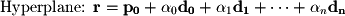
The variables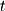 
, 
, and 
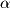are known as free variables and are allowed to range over all possible real scalar values. As they do, the resultant linear combination 
maps out the object. As an example, consider the line mapped out in Figure 4-7.
Object could not be loaded.
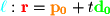
Parameterized Line ()
Given a set of points, how can we determine the parametric form for a line or a plane? Consider a line between two points A and B in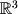 
: 
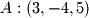and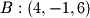 
. Choose one point (arbitrarily) as the starting point and subtract the starting point from the end point to find the vector between the two points. If we take 
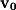as the vector from the origin to A and 
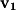as the vector from the origin to B we have the following:
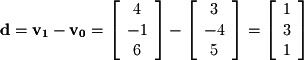
The line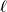 
is defined as an infinite set of vectors starting at 
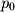along the direction vector 
:
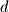